Two Sample t-test
The two sample t-test is used to determine;
whether, the two means of two different samples are equal or not. Before
applying the two sample t-test, First the two sample must follow the normal
distribution. Second, the variance of the two samples must be the same.
Hypothesis:
Ho: There is no difference between
the two samples.
H1: There is a significant
difference between the two samples.
Example:
Considering two filling machines of yoghurt (m1 and m2). We need to test if both machines have the same mean or not in filling the same mass of yoghurt. Following are two samples representing the mass of yoghurt.
|
m1 |
m2 |
|
104.8 |
105.1 |
|
98.8 |
100.3 |
|
101.6 |
106.1 |
|
100.4 |
101.8 |
|
100.7 |
102.5 |
|
99.4 |
103.2 |
|
104.9 |
103.2 |
|
98.7 |
102.9 |
|
102.6 |
105.8 |
|
100.7 |
103.4 |
|
101.7 |
101 |
|
99.5 |
102.6 |
|
98.7 |
101.2 |
|
104.8 |
99.6 |
|
98.9 |
101.6 |
|
100 |
100.4 |
|
98.2 |
105.5 |
|
101.2 |
100.2 |
|
104.2 |
104.3 |
|
101.1 |
103 |
|
104.7 |
99.2 |
|
103.9 |
105.7 |
|
101.8 |
99.1 |
|
98.3 |
100 |
|
105.3 |
|
|
102.6 |
Using R, as shown in the figure
below, the normality of the two data were checked as shown in the box plot.
Using the F-test, it can be concluded that the two variances are the same.
Thus, two-paired t-test can be used to check the means between the two yoghurt
filling machines.
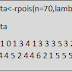
Using R console, use the following command:
(Ttest=t.test(yoghurt$m1,yoghurt$m2,var.equal=T))
From
the below code, it can be seen that the p-value=0.04<0.05, then we reject Ho
and accept H1. There is a significant difference between the two machines.
 |

0 Comments